Before this, see 2024/06/17 Conducting Multi-Round Conversation with Transformers for why we need cache. But we have query, key, value three matrices. Why do you only cache past keys and values? How about past queries?
Attention Mechanism in Detail
Recall the attention process in transformer can be written in the following matrix form: $$ Z = \text{Attention}(Q,K,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V $$ If we look a particular output at position i, it can be written as: $$ z_i =( {})
\begin{bmatrix}
v_1 \\
v_2 \\
\vdots \\
v_n
\end{bmatrix}$$ A simple example can be found in the famous Illustrated Transformer
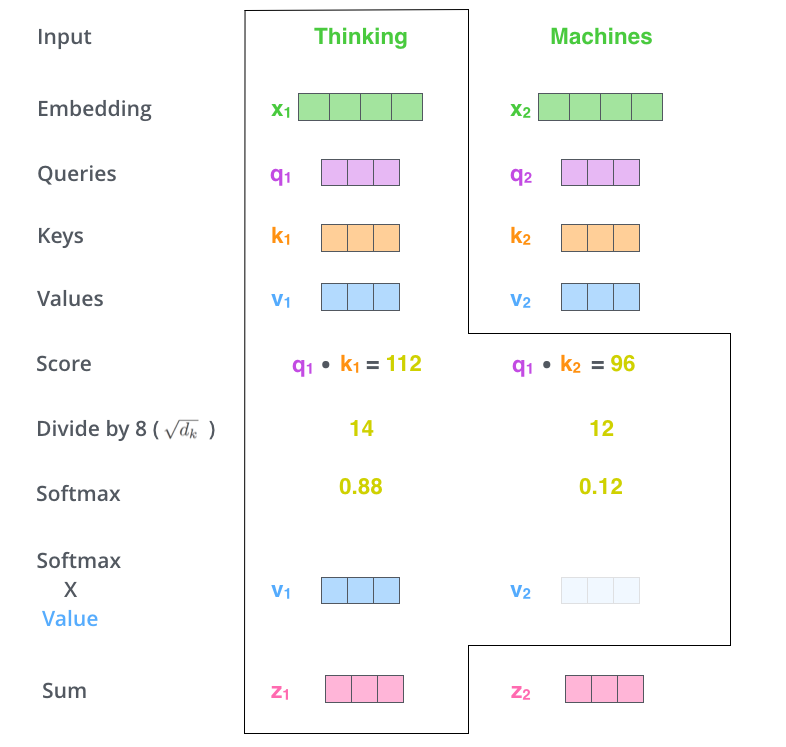
From the formula and the example, we can see that key and values are always a pair in calculation. In fact, this is aligned with the very concept of soft dictionary behind attention: we get a query from somewhere and look at all the keys in the dictionaries to find, for each key, how much it relates to this query and output the weighted average of each key’s value based on the relatedness.
Generative Transformer (Decoder Based)

Let’s consider a causal language model, aka a transformer’s autoregressive generative decoder. At inference time, we only care about the output at the last position because the model is autoregressive and the outputs at all the previous positions are exactly the same as our input. (See the above graph from blogpost Transformers-based Encoder-Decoder Models) Therefore, if the current sequence has length s, we only care about zs. All the other outputs z1…s − 1 are useless.
Inference code in Karpathy’s nanoGPT corroborated this in its inference time implementation:
1 | if targets is None: |
)
\begin{bmatrix}
v_1 \\
v_2 \\
\vdots \\
v_s
\end{bmatrix}$$ It should be clear that to save computation, we only need to cache
the kv values in the previous positions and it’s useless to
cache the q value.
To give a more detailed example, let’s consider the whole process to
generate a sequence of tokens with length n: t1, …, tn.
We can see the previous queries are never used in the computation.
$$ $$
Time Complexity Boost
People complain about the slow inference time of generative transformer model, where it has a quadratic sequence length term O(s2). This quadratic term is caused by QKT matrix multiplication in attention where both matrices have shape s × d. Recall running time of matmul AB where $A \in \R^{m \times p}, B \in \R^{p \times n}$ is O(mpn), so this matmul of query and key matrix has time complexity O(s2d).
However, by observing that we only need the output at the very last position in generative model and utilizing KV-cache, we reduce our matrix $Q \in \R^{s \times d}$ to a single vector of $q \in \R^{1 \times d}$ and effectively reduce the time complexity of this operation to O(sd). Therefore, we can eliminate the quadratic term from our inference time and only need linear time s instead.
What about Encoder Based Transformer Model?
Encoder Based transformer models do not have the issue of repeatedly computing the same past tokens’ attention scores so do not need a KV-cache.
Code Implementation
Facebook’s cross-lingual language model (XLM) gives a fantastic example of how to implement KV-Cache (or transformers in general, it provides abundant comments of tensor shape at each step).
At inference time, do not recompute elements (where
slenor a more descriptive naming can becached_sequence_lengthis how many previous positions have been cached): link1
2
3
4
5
6
7
8if cache is not None:
_slen = slen - cache['slen']
x = x[:, -_slen:]
positions = positions[:, -_slen:]
if langs is not None:
langs = langs[:, -_slen:]
mask = mask[:, -_slen:]
attn_mask = attn_mask[:, -_slen:]Retrieve, use and update cache: link1 link2
1
2
3
4
5
6
7if self.layer_id in cache:
k_, v_ = cache[self.layer_id]
k = torch.cat([k_, k], dim=2) # (bs, n_heads, klen, dim_per_head)
v = torch.cat([v_, v], dim=2) # (bs, n_heads, klen, dim_per_head)
cache[self.layer_id] = (k, v)
...
cache['slen'] += tensor.size(1)
XLM can serve multiple purposes including as a generative causal
language model, masked language model, or a translation language model.
We use KV-Cache only with causal language model in
generate() function, see code.
XLM has a Memory module that implements Product-Key
Memory Layers whose mechanism rings very familiar to me but I can’t
recall where I’ve encountered something similar before. Anyway, you can
ignore those Memory implementations and focus on the
attention part if use it as a source to learn cache or the basics of
attention.
More Code Examples
- This Medium post KV
caching explained leads way to where to find Hugging Face’s
implementation in general, which can be too modular and abstract
nowadays. It’s hidden in the
forwardfunction inXXXForCausalLM. TakeLlamaForCausalLMas an example, in itsforwardfunction, we still need to go down the abstraction toLlamaModel->LlamaDecoderLayer->LlamaAttentionand we can see thepast_key_valuethere implementing theCacheclass. I didn’t read into how Hugging Face did it. - This Zhihu post explaining KV-Cache leads way to Hugging Face’s GPT-2. The original GPT-2 code is in fact more straightforward, but you’d better just read XLM. It simply has more comments and the naming is more self-explanatory.
PS
I initially didn’t find where Hugging Face implemented KV-Cache in
current version (transformer 4.40) but only this Cache
class and failed to find where it’s used. So I followed the
recommendation under this Zhihu post to go
to transformer 2.5.0 instead. A quick search like “kv” or “cache” led me
to modeling_xlm.py.
I was surprised to find early Hugging Face model code was more of a
rename of original implementation instead of a refactor they do now.
I then read this KV caching explained post. Its graph isn’t super straightforward but it introduces how KV-cache reduces time complexity and where to find Hugging Face’s implementation.