Model Selection Tricks

Overfitting and Underfitting¶

There are two problematic cases which can arise when learning a classifier on a data set: underfitting and overfitting, each of which relate to the degree to which the data in the training set is extrapolated to apply to unknown data:

• Underfitting: The classifier learned on the training set is not expressive enough (i.e. too simple) to even account for the data provided. In this case, both the training error and the test error will be high, as the classifier does not account for relevant information present in the training set.
• Overfitting: The classifier learned on the training set is too specific, and cannot be used to accurately infer anything about unseen data. Although training error continues to decrease over time, test error will begin to increase again as the classifier begins to make decisions based on patterns which exist only in the training set and not in the broader distribution.

Identify Regularizer $\lambda$¶

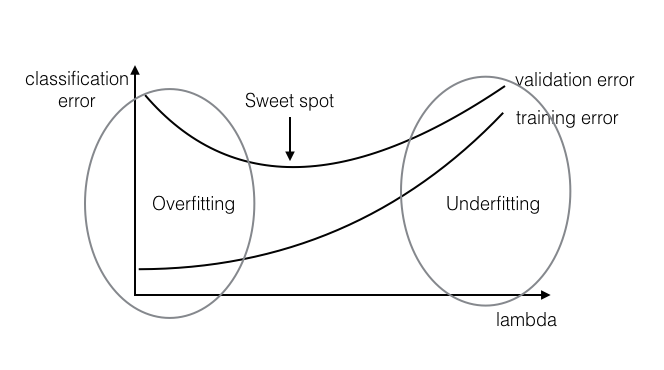
Figure 1: overfitting and underfitting. Note the x-axis is $\lambda$:

• the bigger $\lambda$ is, the simpler the model is, so is likely to underfit.
• the smaller $\lambda$ is, the more complex the model is, so is more likely to overfit

K-Fold Cross Validation¶

When we train the data, we can use the k-fold cross validation: divide the training data into $k$ partitions. Train on $k-1$ of them and leave one out as validation set. Do this $k$ times (i.e. leave out every partition exactly once) and average the validation error across runs. This gives you a good estimate of the validation error (even with standard deviation).

In the extreme case, you can have $k=n$, i.e. you only leave a single data point out (this is often referred to as LOOCV - Leave One Out Cross Validation). LOOCV is important if your data set is small and cannot afford to leave out many data points for evaluation.

We can also use k-fold cross validation solely to determine the hyperparameter $\lambda$: divide data into $k$ partitions, each with a specific $\lambda$; and we will select the $\lambda$ that gives the best validation error.

No matter what we use k-fold for, after selecting the best model/parameter based on k-fold, we will have to train our model on the whole dataset for another time (remember we divided it into $k-1$ training set and 1 validation set), and use that as our final model.

Telescopic search¶

Do two searches:

1. find the best order of magnitude for $\lambda$. 先搜索数量级
2. do a more fine-grained search around the best $\lambda$ found so far. 再搜索此数量级下的最好值

For example, first you try $\lambda=0.01,0.1,1,10,100$. It turns out 10 is the best performing value. Then you try out $\lambda=5,10,15,20,25,...,95$ to test values “around” 10.

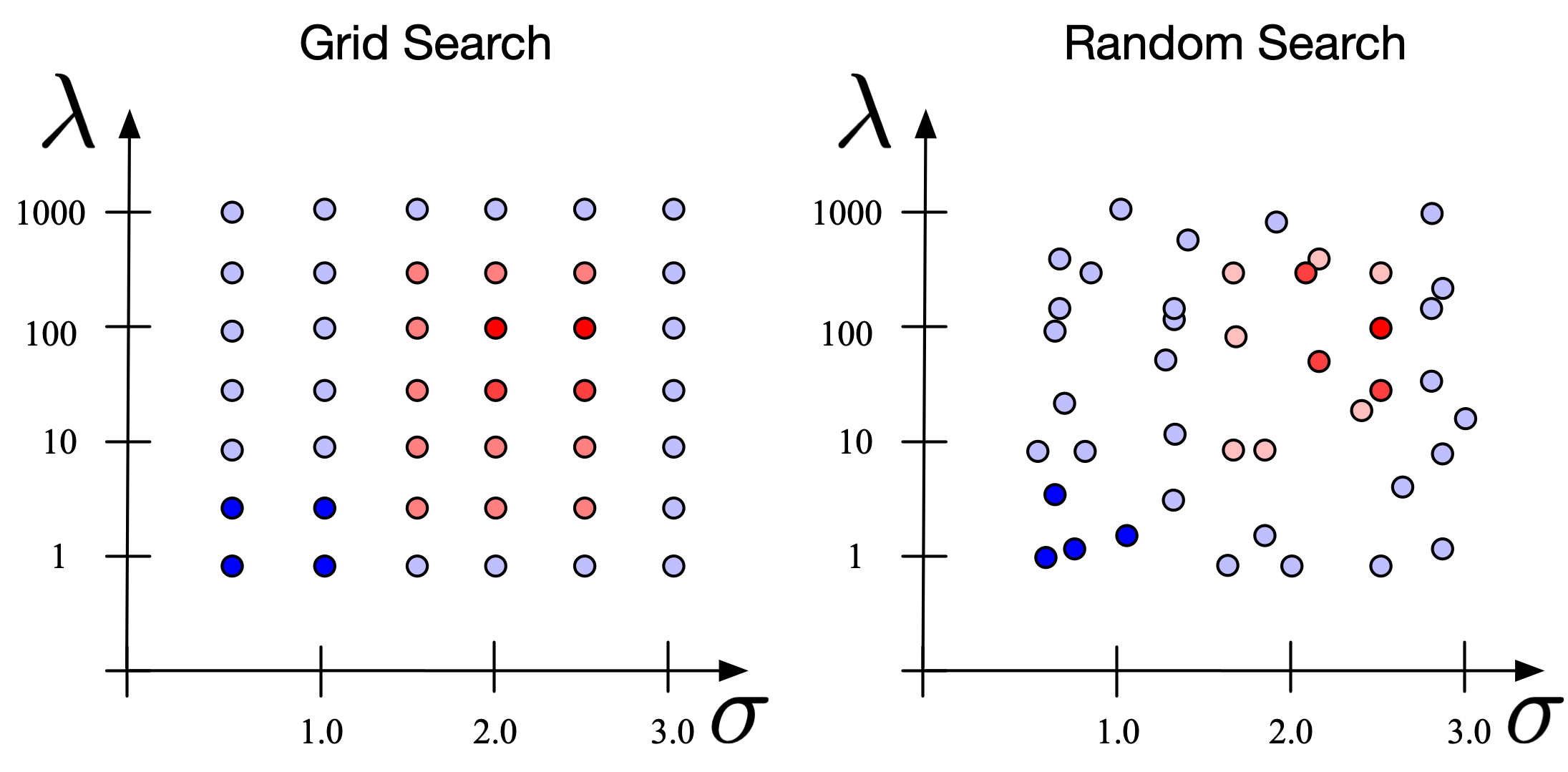
Grid and Random search¶

• Grid Search: If you have multiple parameters (e.g. $\lambda$ and also the kernel width $\sigma$ in case you are using a kernel) a simple way to find the best value of both of them is to fix a set of values for each hyper-parameter and try out every combination. 在 grid 上顺序选择
• Random Search: Instead of selecting hyper-parameters on a pre-defined grid, we select them randomly within pre-defined intervals. 在区间(也可以理解成 grid)上随机选择

Figure 2: Grid Search vs Random search (red indicates lower loss, blue indicates high loss).

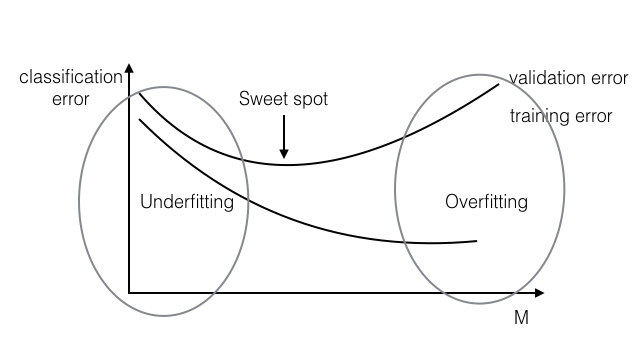
Early Stopping¶

Stop your optimization after M (>= 0) number of gradient steps, even if optimization has not converged yet, because our final model almost always overfits.

实际操作中，边训练边存模型，找到有最小 validation error 的模型（即我们不一定用最终的模型，相当于我们提早结束了训练)

Figure 3: Early stopping，注意这里和前图 1 不一样，横轴是 M