Principal Component Analysis

PCA finds the low dimensional structure of high dimensional data.

Basic Ideas¶

Whereas k-means clustering sought to partition the data into homogeneous subgroups, principal component analysis (PCA) will seek to find, if it exists, low-dimensional structure in the data set $\{ x\}_{i = 1}^{n}$ ($x_{i} \in \mathbb{R}^{d}$). The features in which the data vary the most describes this lower-dimensional subspace.

PCA finds a low-dimensional representation of the data that captures most of the interesting behavior. Here, “interesting” will be defined as variability. This is analogous to computing “composite” features (i.e. linear combinations of entries in each $x_{i}$ that explain most of the variability in the data.)

Take a simple example: if there exists one unit vector $u \in \mathbb{R}^{d}$ such that $x_{i} \approx \alpha_{i}u$ for some scalar $\alpha_{i}$, then we can roughly represent all $x_i$ by a much smaller number of “features.” (in this case only one $u$) If we accept that $u$ is a valid “feature” for all of our data, we could approximate our data using only the scalar $\alpha_{i}$ to describe how $x_i$ behaves on that feature $u$. More concisely, we say that the $x_{i}$ approximately lie in $span\{u\}$, a subspace of dimension 1.

This is illustrated in the next figure, where we see two dimensional data that approximately lies in a one dimensional subspace $span\{v\}$. If we know what $v$ is, we can approximate all data using only $\alpha$.

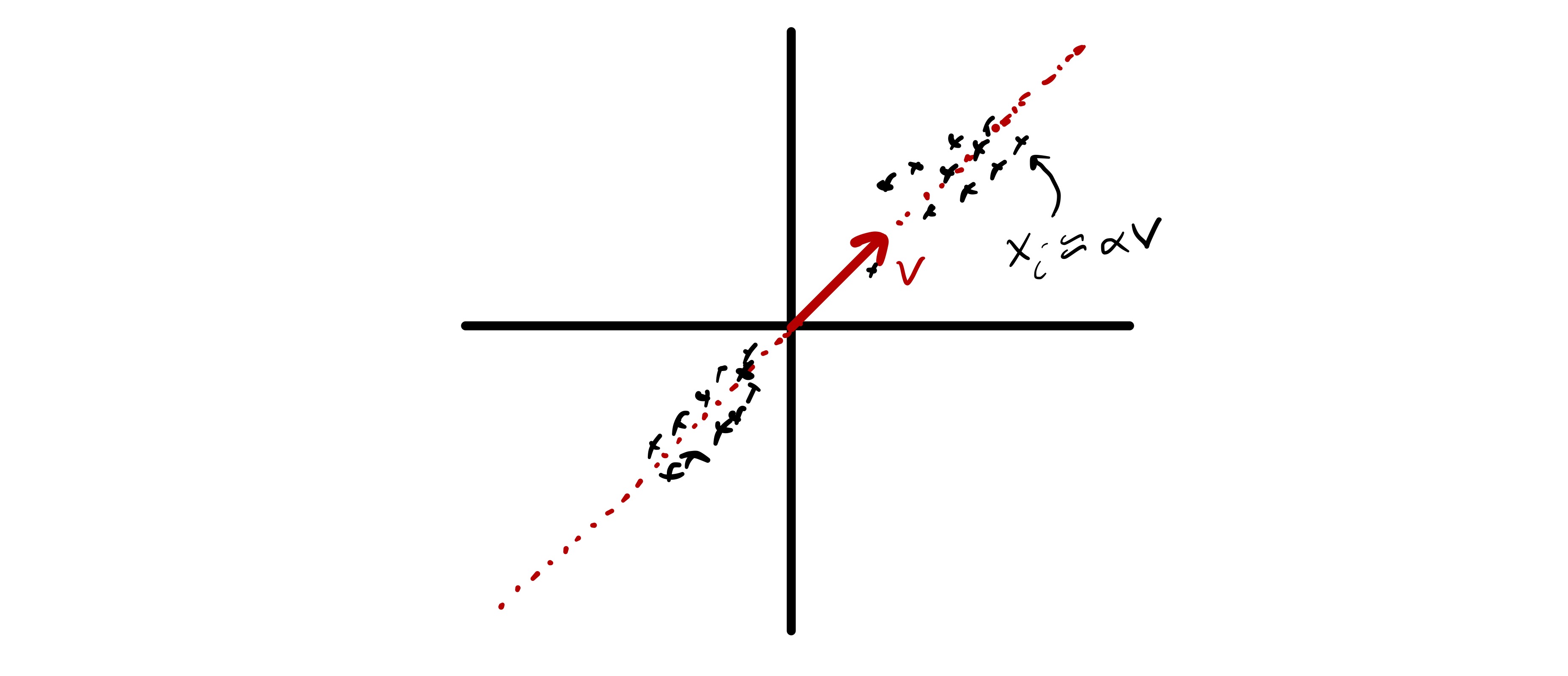
Centering the data¶

Typically in unsupervised learning, we are interested in understanding relationships between data points and not necessarily bulk properties of the data. If the data has a sufficiently large mean, i.e. $\mu = \frac{1}{n}\sum\limits_{i}x_{i}$ is sufficiently far from zero, the best approximation of each data point is roughly $\mu$.

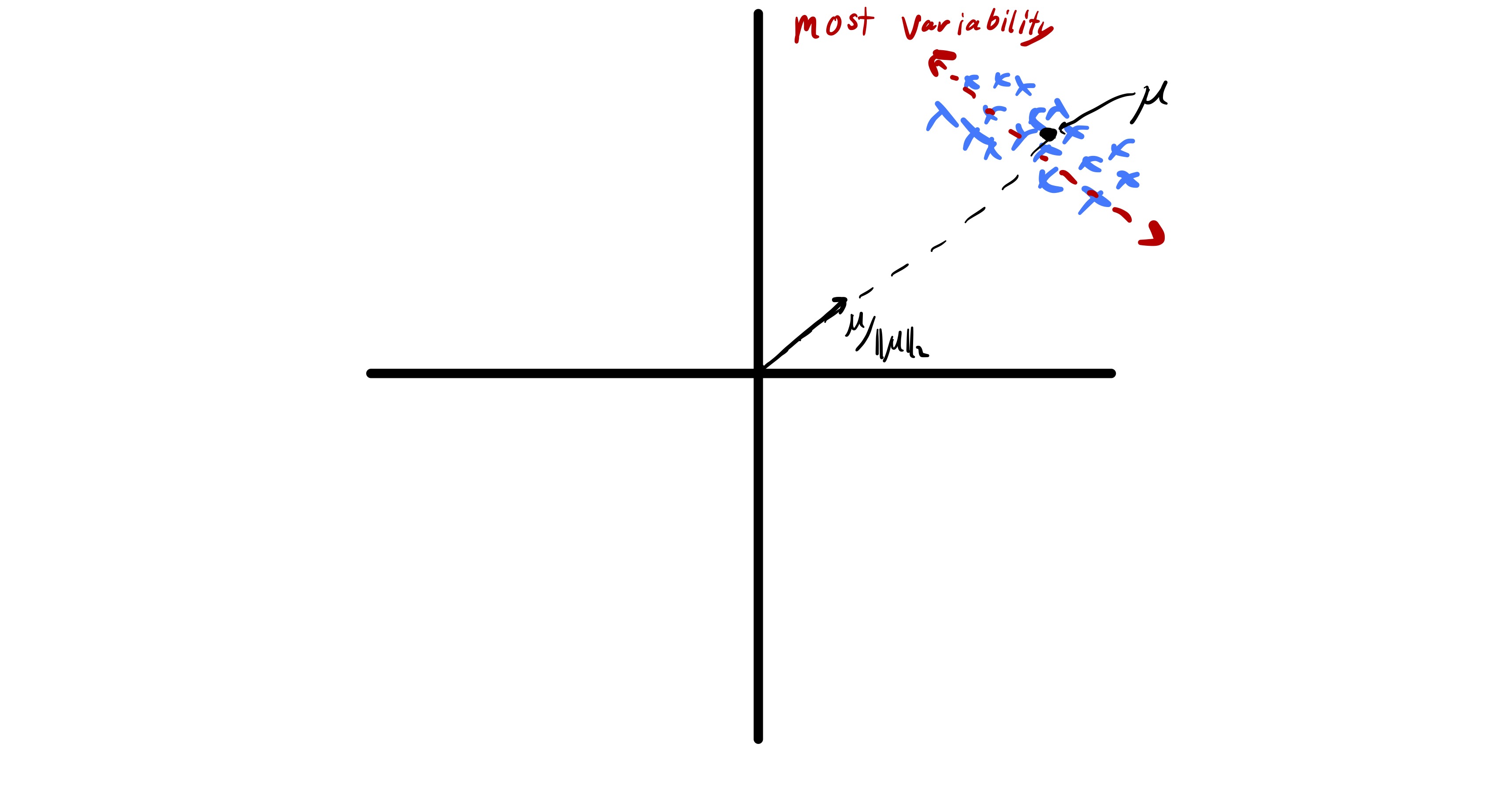
Therefore, to actually understand the relationship between features we would like to center our data before applying PCA by deleting the mean from data. Specifically, we let

where $\mu = \frac{1}{n}\sum\limits_{i}x_{i}.$ We now simply work with the centered feature vectors $\{{\hat{x}}_{i}\}_{i = 1}^{n}$ and will do so throughout the remainder of these notes.

Maximizing the variance¶

Describing Problem¶

To do PCA, we want to find a small set of composite features that capture most of the variability in the data. To illustrate this point, we will first consider finding a single composite feature that captures the most variability in the data set, then proceed to find the 2nd one, 3rd one...

Mathematically, we want to find a vector $\phi = [\alpha_1, \dots, \alpha_d]\in \mathbb{R}^{d}$ such that the sample variance of the scalars

is as large as possible. Note $\phi$ here is the weight: given a data point $x_i$, for each dimension $[x_i]_j$ we assign it a weight $\alpha_j$, so we have a weighted sum across dimension of the original data point $x_i$. We try to come up with a composite feature that varies a lot, so we want to maximize the variance of $z_i$. Note the mean $\hat\mu_z$ of these $z$ is 0 because we did the normalization previous step.

We also have to constrain $\parallel \phi \parallel_{2} = 1$, or we could artificially inflate the variance by simply increasing the magnitude of the entries in $\phi$.

We can now formally define the first principal component of a data set:

First principal component: The first principal component of a data set $\{ x_{i}\}_{i = 1}^{n}$ is the vector $\phi \in \mathbb{R}^{d}$ that solves

$$\max\limits_{\parallel \phi \parallel_{2} = 1}\frac{1}{n}\sum\limits_{i = 1}^{n}(\phi^{T}{\hat{x}}_{i})^{2}$$

(4)

We will consider the data matrix

. This allows us to rephrase the problem as

In other words, $\phi$ is the unit vector that makes the matrix ${\hat{X}}^{T}$ as large as possible.

Solving Problem - 1st PC¶

We will show how to find the first PC (Principal Components) in this section. We can use singular value decomposition (SVD). To simplify this presentation we make the reasonable assumption that $n \geq d.$ We can always decompose the matrix $\hat{X}$ as

where $U$ is a $d \times d$ orthonormal matrix, $V$ is an $n \times d$ orthonormal matrix, $\Sigma$ is a $d \times d$ diagonal matrix with $\Sigma_{ii} = \sigma_{i} \geq 0,$ and $\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{d}$. Remind again we have $n$ data vectors. Each vector has $d$ dimension.

we call $u_{i}$ the left singular vectors, $v_{i}$ the right singular vectors, and $\sigma_{i}$ the singular values. This SVD can be done in $\mathcal{O}(nd^{2})$. 这些都是 SVD 的定义而已

Claim: we achieve $max \parallel {\hat{X}}^{T}\phi \parallel_{2}$ when we have $\phi = u_{1}$.

Proof: Note $U$ is a $d \times d$ orthonormal matrix, so its columns constitute a base of $\mathbb{R}^d$. Since we defined $\phi \in \mathbb{R}^d$, we can write $\phi$ as a combination of these bases:

where $\sum\limits_{i}a_{i}^{2} = 1$ (because we want $\parallel \phi \parallel_{2} = 1$). We now observe

Therefore,

$$

$$

According to assumption $\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{d}$, we achieve max when $a_{1} = 1$ and $a_{i} = 0$ for $i \neq 1$. 证毕

Solving Problem - Other PCs¶

So, the first left singular value of $\hat{X}$ gives us the first principal component of the data. What about finding additional directions? Formally, we want to find $\psi$ such that $y_{i} = \psi^{T}{\hat{x}}_{i}$ has the next most variability. 但我们又不能简单地说 $\psi \not= \phi$, 因为我们可以随便找一个间隔 $\phi$ 非常近的 $\phi$ 即可。 Therefore, we need to force the second PC to be orthogonal to the first, i.e. $\psi^{T}\phi = 0$. We can actually find the second principal component is $\psi = u_{2}$ in our SVD matrix $U$. Fig.11 illustrates how the first two principal components look for a stylized data set. We see that they reveal directions in which the data varies significantly.

More generally, the SVD actually gives us all the principal components of the data set $\{ x_{i}\}_{i = 1}^{n}$.

Principal components: Principal component $\ell$ of data set $\{ x_{i}\}_{i = 1}^{n}$ is denoted $\phi_{\ell}$ and satisfies

$$\phi_{\ell} = u_{\ell}$$

(12)

where $\hat{X} = U\Sigma V^{T}$ is the SVD of $\hat{X}.$

Explaining variability in the data¶

Having obtained the answer, we can look back into our problem $\max\limits_{\parallel \phi \parallel_{2} = 1} \parallel {\hat{X}}^{T}\phi \parallel_{2}$ in a cleaner way.

The equation above helps us recall that we were maximizing the variance of this vector ${\hat{X}}^{T}\phi$ and the maximized variance is the eigenvalue of matrix ${\hat{X}}{\hat{X}}^{T}$. In other words, the singular values reveal the sample variance of $\phi_\ell^Tx_i$. This result generalizes to PCs other than the first one.

If we project our data into the span of the first $k$ eigenvectors, the variance we can achieve is the first $k$ eigenvalues summed up Formally, the total variability of the data captured by the first $k$ PC is $\sum\limits_{i = 1}^{k}\sigma_{i}^{2}$. This is the value we kept with $k$ interesting composite dimension.

One way we determine $k$ - how many vectors we want for PCA is to look at how much of the variance at all dimensions are captured by our $k$ composite interesting dimensions:

We want to pick a relatively small $k$ such that a relatively big ratio can be achieved. In practice, we can do a similar thing as we did with K-Means: we can pick $k$ by identifying when we have diminishing returns in explaining variance by adding more principal components, i.e. looking for a knee in the plot of singular values.

PCA Application¶

We use PCA to reduce dimensions.

A common use of PCA is for data visualization. In particular, if we have high dimensional data that is hard to visualize we can sometimes see key features of the data by plotting its projection onto a few (1, 2, or 3) principal components. For example, if $d = 2$ this corresponds to forming a scatter plot of $(\phi_{1}^{T}{\hat{x}}_{i},\phi_{2}^{T}{\hat{x}}_{i})$.